[트리의 지름을 이루는 두 정점] 귀류법을 통한 증명
[트리의 지름 구하기]
트리에서 지름이란, 가장 먼 두 정점 사이의 거리 혹은 가장 먼 두 정점을 연결하는 경로를 의미합니다. 선형 시간안에 트리에서 지름을 구하는 방법은 다음과 같습니다.
- 트리에서 임의의 정점 i를 잡습니다.
- 정점 i에서 가장 먼 정점 u를 찾습니다.
- 정점 u에서 가장 먼 정점 v를 찾습니다.
트리의 지름은 정점 u와 정점 v를 연결하는 경로입니다.
여기서 증명은 귀류법을 통해서 증명합니다.
트리의 지름을 이루는 두 정점을 u,v라고 하고, 임의의 정점 i에서 가장 멀리 떨어진 정점을 A라고 합시다.
여기서 A가 트리를 이루는 정점이 아니라고 가정해봅시다. 그렇다면, dist(u,i)+dist(v,i) > dist(u,i) + dist(A,i)를 만족해야합니다.
하지만 A는 i에서 가장 멀리 떨어진 정점이므로 모순됩니다. 따라서 임의의 점 i에서 가장 멀리 떨어진 정점은 반드시, 트리의 지름을 이루는 정점 중 하나가 됩니다. 그 하나를 찾으면 나머지 하나는 또 그 정점에서 가장 멀리 떨어진 정점을 찾으면 됩니다.
아래 그림을 보며 이해해봅시다.
u와 v를 트리의 지름을 이루는 두 정점이라고 합시다. 임의의 정점 i를 정하고 임의의 정점 A를 정합니다. (A는 i에서 가장 멀리 떨어진 정점입니다). 다음 그림을 보면 A를 u와v가 아닌 다른 가장 깊은 정점을 찾았습니다. 이걸 u,v를 잇는 직선에 회전시켜 겹치게 합니다.
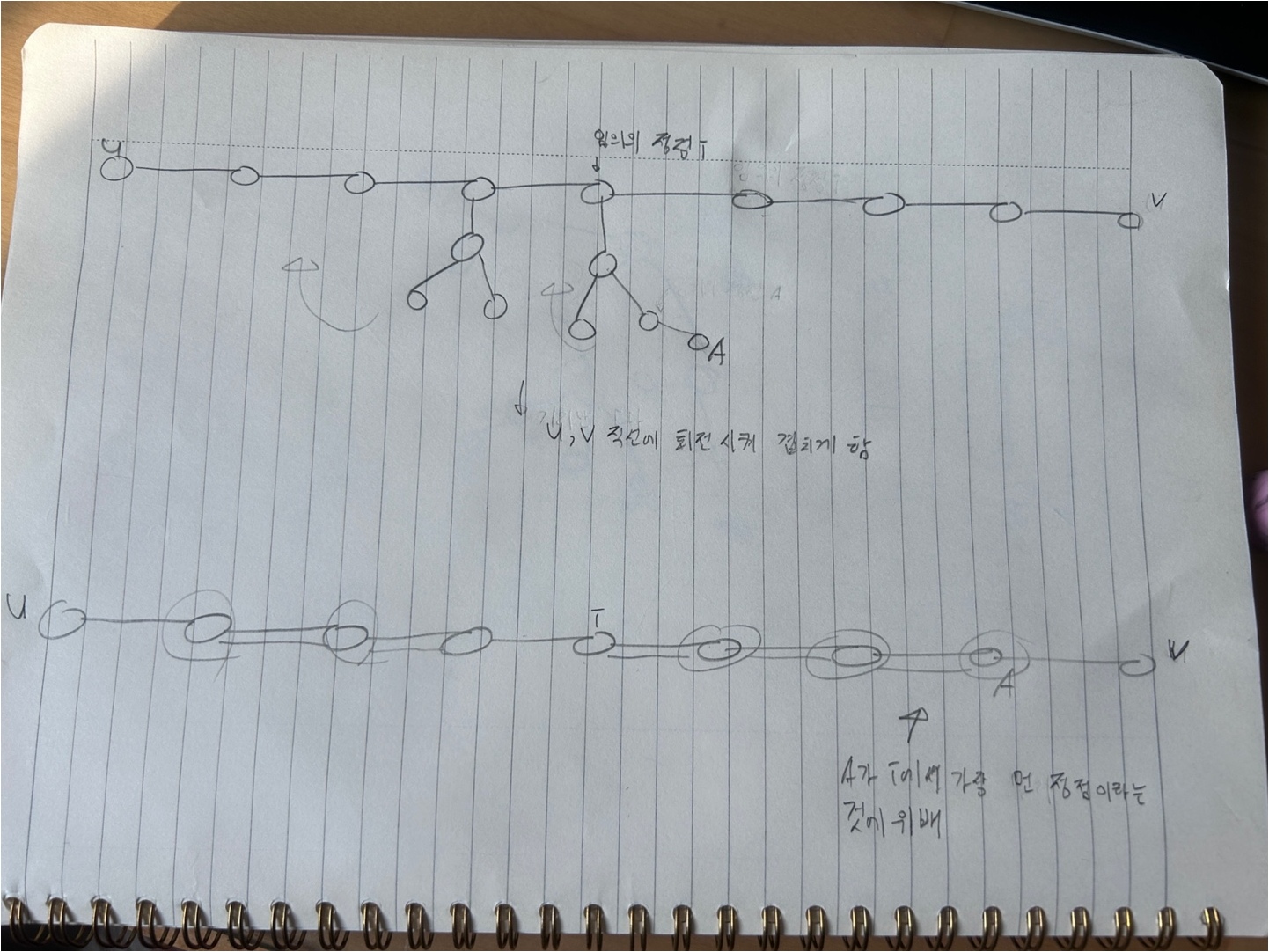
그러면 A가 i에서 가장 먼 정점이라는 사실에 위배됩니다. 이는 그림에서 임의로 잡은 i와 A가 아니더라도 어떻게 잡든지 간에 위배가 됩니다. 따라서 임의의 정점 i에서 가장 먼 정점은 트리의 지름을 이루는 정점 중 하나가 됩니다.