[Rasterization] 스크린좌표계에서 정확한 원근투영 interpolation지점 찾기

일반적으로 레스터화에서 정투영, 원근투영 모두 월드좌표계의 vertex들을 스크린 좌표계로 변환시킨 후 barycentric coordinates(무게중심좌표계)를 이용하여, uv좌표를 찾고 fragment에 알맞은 색을 입힙니다. 하지만 정투영에서는 왜 문제가 안 생기고, 원근투영에서 문제가 생길까요? 다음 그림을 보며 이상한 부분을 발견해봅시다.

 

 

 

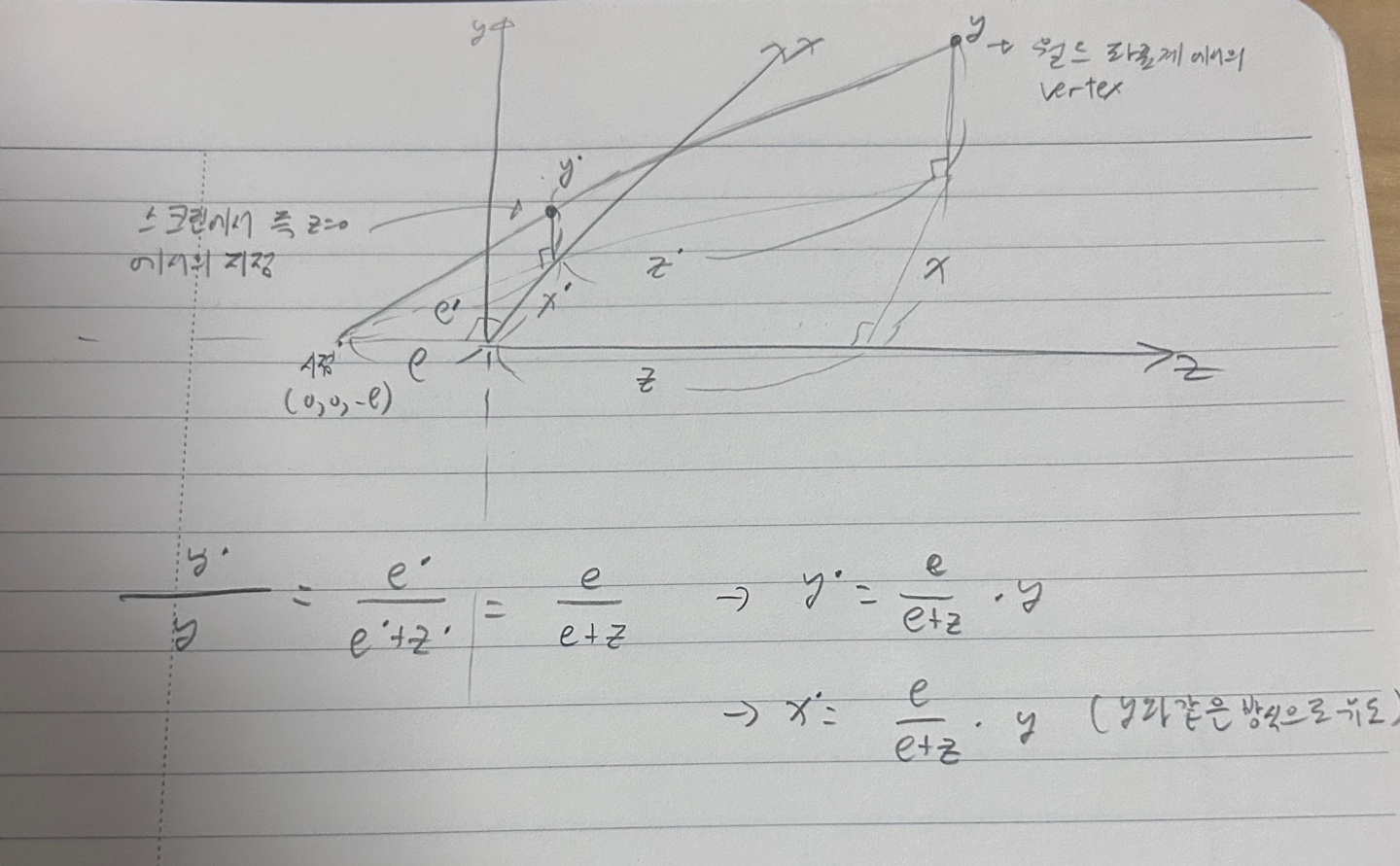
격자무늬가 삐뚤어져있죠? 원래 월드좌표계에서의 모습은 잘 정렬되어져 있는 모습입니다. 왜 왜곡되게 보이는지 원리를 이해하기전에 레스터화에서 원근투영의 원리를 천천히 이해해봅시다. 다음 그림과 같이 레스터화의 원근투영은 월드좌표계의 vertex를 스크린좌표계 즉 z=0일 때로 투영시킨 지점을 찾습니다. (닮은꼴을 통해 구합니다)

 

 

 

Raytracing은 ray를 픽셀에 쏴서, 해당 물체에 맞으면 그 hit값을 반환시켜 픽셀에 색을 할당하는 원론적인 방식을 이용하여 왜곡이 일어나지 않는데요. 그와달리 레스터화에서는 기본적으로 월드좌표계의 삼각형을 스크린 좌표계로 투영합니다. 그리고 픽셀의 위치를 레스터좌표계로 변환된 삼각형의 vertex를 이용하여 barycentric coordinate를 통해 위치를 구해냅니다. 여기서 왜곡이 생긴다는 점입니다. 왜 왜곡이 생기는지 이해가 안가시는게 당연합니다. 

예를들어 다음 그림을 봅시다.

 

A와 B를 스크린좌표계로 투영시킨 후 K'를 barycentric coordinates로 찾아낸다고 생각해봅시다. A'와 B'의 K'는 아마 3대1비율정도로 보이시죠? 그런데 우리가 원하는 것은 1대1 비율이었던 것입니다. A와B의 중간이 K이기 때문이죠. 정확한 위치는 1대1비율입니다. A'와 B'사이의 K'를 3대1비율로 구해서 frament에 색을 입힌다면, 1대1이아니라서 당연히 왜곡이 일어날 것입니다. 예를들어 A가 Red이고, B가 Green이었다면 원하는 색은 1대1 즉, 노란색인데, 3대1이라 주황색이 나올 수 있다는 것입니다.

 

즉 우리가 원하는 것은 K'의 barycentric coordinate를 통해 A와 B사이에 있는 K의 barycentric coordinate를 찾는 것입니다!  아래 그림으로 증명을 하였습니다. 구해야하는 p는 아직 미지수입니다. 하지만, p'가 결정되어있고 , a,b,c에 의한 평면도 결정되어있다는 뜻이니 잘 풀어내면 반드시 p를 구할 수 있습니다.

이렇게 a,b,c사이의 p의 barycentric coordinate를 구하였습니다. 다음 논문을 참고하였습니다.

논문과 해설글

// Perspective-Correct Interpolation
// 논문
// https://www.comp.nus.edu.sg/~lowkl/publications/lowk_persp_interp_techrep.pdf
// 해설글
// https://www.scratchapixel.com/lessons/3d-basic-rendering/rasterization-practical-implementation/perspective-correct-interpolation-vertex-attributes

 

 

여기서 이제 α,  β,  Γ 는 어떻게 구할까요? a'와 a가 1 : α라는 점을 이용하면 됩니다. 이 글의 두번째 그림을 보면, 시점과 화면사이의 거리 e와 z값으로 비율을 구했습니다. 따라서 이와같은 원리를 통해  e : e + z = 1 : α를 알 수있고 따라서 α는 (e + z) / e가 됩니다.  β,  Γ또한 마찬가지입니다. 간단히 코드로 표현하면 다음과 같습니다.

 

 if (w0 >= 0.0f && w1 >= 0.0f && w2 >= 0.0f) {

     const float z0 = (this->vertexBuffer[i0].z + distEyeToScreen)/distEyeToScreen;
     const float z1 = (this->vertexBuffer[i1].z + distEyeToScreen)/distEyeToScreen;
     const float z2 = (this->vertexBuffer[i2].z + distEyeToScreen)/distEyeToScreen;

     if (this->usePerspectiveProjection &&
         this->usePerspectiveCorrectInterpolation) {

         // w0, w1, w2를 z0, z1, z2를 이용해서 보정
         w0 /= z0;
         w1 /= z1;
         w2 /= z2;

         const float wSum = w0 + w1 + w2;

         w0 /= wSum;
         w1 /= wSum;
         w2 /= wSum;
     }

     // 이하 동일
     const float depth = w0 * z0 + w1 * z1 + w2 * z2;
     const vec3 color = w0 * c0 + w1 * c1 + w2 * c2;
     const vec2 uv = w0 * uv0 + w1 * uv1 + w2 * uv2;

     if (depth < depthBuffer[i + width * j]) {
         depthBuffer[i + width * j] = depth;

         PSInput psInput;
         psInput.color = color;
         psInput.uv = uv;

         pixels[i + width * j] = MyPixelShader(psInput);
     }

 

 

강의 출처 : 홍정모 그래픽스 새싹코스 part2

https://honglab.co.kr/collections

honglab